diff options
Diffstat (limited to 'notes/rasterizing-triangles.md')
| -rw-r--r-- | notes/rasterizing-triangles.md | 2 |
1 files changed, 1 insertions, 1 deletions
diff --git a/notes/rasterizing-triangles.md b/notes/rasterizing-triangles.md index 73acb33..88f232a 100644 --- a/notes/rasterizing-triangles.md +++ b/notes/rasterizing-triangles.md @@ -31,7 +31,7 @@ In order to figure out how build this rasterizer [I reached out to the internet] From this comment you can see that it is trivial to calculate to calculate the barycentric coordinates of the triangle from the edge function. You simply need to divide the the calculated edge function value by the area of parallelogram. Now what is the area of triangle? Well this is where some [more research](https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-rendering-a-triangle/barycentric-coordinates) online helped. If the edge function defines the area of a parallelogram (2 times the area of the triangle) of `(X,Y)->(X+dX,Y+dY)` and `(X,Y)->(x,y)`, and we calculate three edge function values (one for each edge), then we have 2 times the area of each of the sub triangles that are defined by our point. -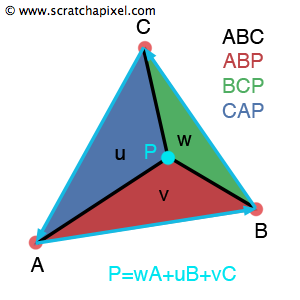 + From this its trivial to see that we can calculate 2 times the area of the triangle just by adding up all the individual areas of the sub triangles (I used triangles here, but really we are adding the area of sub parallelograms to get the area of the whole parallelogram that has 2 times the area of the triangle we are drawing), that is adding the value of all the edge functions together. From this we can see to linear interpolate any value on the triangle we can use the following equation |